Article Writing a graphical shell in Python - part 3
Part 1 Part 2
Hello everyone!
In the previous parts, we got acquainted with two methods of positioning elements - pack () and place (). They are fine for simple tasks. And if we are planning a program with a complex interface, or just a large number of elements, then the best method is undoubtedly grid (). At first glance, the method is a little more complicated, but once you figure it out, it won't look complicated.
The grid () method, as the name implies, is a grid. It looks like this schematically:
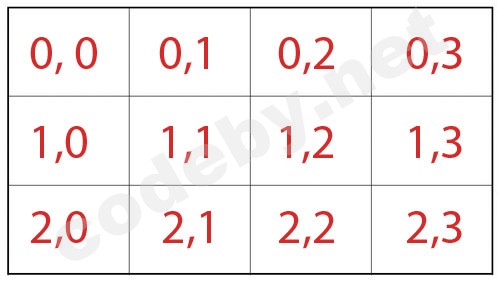
That is, the program window is divided into columns and rows, and the numbering starts from zero. And before you start programming, it is best to draw the future program on an ordinary piece of paper in the box. This will give you a complete idea of which cells to put what. Columns and rows can be concatenated using columnspan and rowspan.
For example, let's throw in a simple calculator, and the lined drawing will help you navigate in columns and rows.
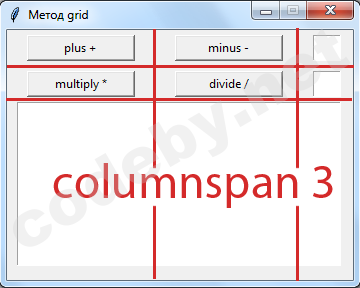
Here we have 4 buttons for calculating addition, subtraction, multiplication and division, as well as 2 one-line text fields for entering numbers. And the bottom will show the calculation results in a multi-line text box. As you can see, a multi-line field is 3 columns wide, so you need to combine the columns using columnspan.
According to the first plate, it is easy to understand that, for example, the minus button is in line 0 and column 1. Now let's see the code. Since the buttons come from the top-left corner, that's where you need to start.
The essence of the writing method differs little from the previous ones. After creating any element, we specify the method with the next line through a period, and write positioning according to the grid + make the necessary indents, and you can also specify the orientation to the cardinal points using sticky. Next we have one-line text fields for data entry.
And the main window ends with a multi-line text field. Everything is the same - field size + positioning, and in this case, the combination of columns.
Well, for all this economy to work, you need to write functions that will do calculations when you click on the corresponding buttons.
Please note that since we perform mathematical operations with integers, we wrap the data received from the fields with numbers in int. And so that the calculation results are on a new line each time, we added a line break '\ n'. But since strings and numbers cannot be together when inserting calculations into a field, we first translate the results of calculations into a string using str.
Now let's check the functionality of the program. Let's start and do all the calculations in turn. Everything is working.

So we figured out the grid () method, as you can see, nothing complicated. This is the method I use in most cases.
Now for your homework .
Continue with the calculator by adding 3 buttons - exponentiation, exponentiation , rootin, and Clean to clear the multiline field.

In this example, I first entered 3 and 4, did the calculations, and to check if the exponentiation and root extraction work correctly for us, I entered 81.3
to 4 powers = 81 and extraction from 81 roots of 4 degrees = 3 That's right.
Hello everyone!
In the previous parts, we got acquainted with two methods of positioning elements - pack () and place (). They are fine for simple tasks. And if we are planning a program with a complex interface, or just a large number of elements, then the best method is undoubtedly grid (). At first glance, the method is a little more complicated, but once you figure it out, it won't look complicated.
The grid () method, as the name implies, is a grid. It looks like this schematically:
That is, the program window is divided into columns and rows, and the numbering starts from zero. And before you start programming, it is best to draw the future program on an ordinary piece of paper in the box. This will give you a complete idea of which cells to put what. Columns and rows can be concatenated using columnspan and rowspan.
For example, let's throw in a simple calculator, and the lined drawing will help you navigate in columns and rows.
Here we have 4 buttons for calculating addition, subtraction, multiplication and division, as well as 2 one-line text fields for entering numbers. And the bottom will show the calculation results in a multi-line text box. As you can see, a multi-line field is 3 columns wide, so you need to combine the columns using columnspan.
According to the first plate, it is easy to understand that, for example, the minus button is in line 0 and column 1. Now let's see the code. Since the buttons come from the top-left corner, that's where you need to start.
Python:
plus_button = Button(text="plus +", width=14, command=plus)
plus_button.grid(row=0, column=0, padx=10, pady=5, sticky="n")
minus_button = Button(text="minus -", width=14, command=minus)
minus_button.grid(row=0, column=1, padx=10, pady=5, sticky="n")
multiply_button = Button(text="multiply *", width=14, command=multiply)
multiply_button.grid(row=1, column=0, padx=10, pady=5, sticky="n")
split_button = Button(text="divide /", width=14, command=split)
split_button.grid(row=1, column=1, padx=10, pady=5, sticky="n")
Python:
first_number = Entry(width=4, justify=CENTER)
first_number.grid(row=0, column=2, pady=5, sticky="ns")
two_number = Entry(width=4, justify=CENTER)
two_number.grid(row=1, column=2, pady=5, sticky="ns")
Python:
text = Text(root, width=40, height=10)
text.grid(row=2, column=0, columnspan=3, padx=10, sticky='nswe')
Python:
def plus():
a = int(first_number.get())
b = int(two_number.get())
res = str(a+b)
text.insert(END, res + '\n')
def minus():
a = int(first_number.get())
b = int(two_number.get())
res = str(a - b)
text.insert(END, res + '\n')
def multiply():
a = int(first_number.get())
b = int(two_number.get())
res = str(a * b)
text.insert(END, res + '\n')
def split():
a = int(first_number.get())
b = int(two_number.get())
res = str(a / b)
text.insert(END, res + '\n')
Python:
from tkinter import *
root = Tk()
root.title("Метод grid")
root.geometry("346x250")
root.resizable(width=False, height=False)
def plus():
a = int(first_number.get())
b = int(two_number.get())
res = str(a+b)
text.insert(END, res + '\n')
def minus():
a = int(first_number.get())
b = int(two_number.get())
res = str(a - b)
text.insert(END, res + '\n')
def multiply():
a = int(first_number.get())
b = int(two_number.get())
res = str(a * b)
text.insert(END, res + '\n')
def split():
a = int(first_number.get())
b = int(two_number.get())
res = str(a / b)
text.insert(END, res + '\n')
plus_button = Button(text="plus +", width=14, command=plus)
plus_button.grid(row=0, column=0, padx=10, pady=5, sticky="n")
minus_button = Button(text="minus -", width=14, command=minus)
minus_button.grid(row=0, column=1, padx=10, pady=5, sticky="n")
multiply_button = Button(text="multiply *", width=14, command=multiply)
multiply_button.grid(row=1, column=0, padx=10, pady=5, sticky="n")
split_button = Button(text="divide /", width=14, command=split)
split_button.grid(row=1, column=1, padx=10, pady=5, sticky="n")
first_number = Entry(width=4, justify=CENTER)
first_number.grid(row=0, column=2, pady=5, sticky="ns")
two_number = Entry(width=4, justify=CENTER)
two_number.grid(row=1, column=2, pady=5, sticky="ns")
text = Text(root, width=40, height=10)
text.grid(row=2, column=0, columnspan=3, padx=10, sticky='nswe')
root.mainloop()Now let's check the functionality of the program. Let's start and do all the calculations in turn. Everything is working.
So we figured out the grid () method, as you can see, nothing complicated. This is the method I use in most cases.
Now for your homework .
Continue with the calculator by adding 3 buttons - exponentiation, exponentiation , rootin, and Clean to clear the multiline field.
In this example, I first entered 3 and 4, did the calculations, and to check if the exponentiation and root extraction work correctly for us, I entered 81.3
to 4 powers = 81 and extraction from 81 roots of 4 degrees = 3 That's right.







Commentaires